3.3 Broadband photometry

Physically, the most useful and interesting quantities that one seeks to determine in quantifying upper atmospheric discharges are the electric field $\bf E$ and the electron distribution function $f({\bf v})$. As mentioned in Section 1.3, direct in situ measurement of these or other quantities in the mesosphere and lower ionosphere is rather difficult, as is remote sensing by means of radar [Tsunoda et al., 1998].

The intensity and spectrum of optical emissions from excited neutral and ionized species depend on both $n_{e}$ and ${\bf E}$, providing access to both of these quantities and others which can be derived from them. In the following, we consider the factors affecting long range passive optical remote sensing. A useful spectral emission line should have a radiation lifetime as fast as the variations in electric field due to a VLF pulse, for reasons discussed in Section 1.3, and fast compared to the time scale for relaxation of the electron distribution function . As it turns out, the primary emissions from elves come from excited states with lifetimes of $\sim$6 $\mu$s and $<$1 $\mu$s (Section 2.4.3), while the electron distribution thermalizes in $\sim$10 $\mu$s.

When enough natural signal is available, it is desirable to achieve maximum spectral, as well as temporal, resolution. Spectra of sprites have been measured [Heavner, 2000; Mende et al., 1995; Hampton et al., 1996], but the limited total optical output in elves is not conducive to spectrophotometric measurements. More practical alternatives for detecting a band of spectral lines such as ${\rm N}_2(1{\rm P})$ are either to (1) use very narrow optical filters to maximise the signal to noise ratio obtainable from a single spectral line, or, if such a signal is insufficient to overcome fundamental instrument noise or an adequately narrow filter is not available, (2) a broadband filter may be used to benefit from the extra signal available over several spectral lines of a given molecular band. This latter strategy was pursued for high time resolution photometry of elves, and more than one such filter is used on different photometers to achieve at least some spectral information. Section 3.3 treats the subject of broadband photometric measurements.

In the following, we define the surface brightness which is used in all optical observations reported in this dissertation, and discuss the calibration of an instrument (such as the Fly's Eye) with a broadband optical response.

3.3.1 Surface Brightness

The brightness in Rayleighs of an optical transition line is defined as [Chamberlain, 1978, p. 213]

$$I_k = 10^{-6} \int A_k n_k dr,$$ (3.1)

where $n_k$ is the number density [cm$^{-3}$] of excited particles in state $k$, $A_k$ is the radiation transition rate [s$^{-1}$] mentioned in Section 2.4.3, and the integral is taken over the line of sight [cm]. The units of $I_k$ as given in (3.1) are 10$^{6}$ photons-s$^{-1}$cm$^{-2}$str$^{-1}$. The radiation is assumed to be isotropic.

Figure 3.5: General geometry of a photometer and extended source.

A photometer with an optical aperture $A$ and a field-of-view subtending a solid angle $\Omega$$\ll$1 responds to optical emissions along its line of sight, as shown in Figure 3.5. Let a unit volume of the optical source isotropically radiate photons at rate ${\mathcal F}(\lambda)d\lambda$ in the wavelength range $\lambda$ to $\lambda$+$d\lambda$; that is,

$${\mathcal F}(\lambda)=\sum_k A_k(\lambda) n_k.$$ (3.2)

Here $A_k(\lambda)$ is now the radiation transition rate per unit wavelength [for example in units of s$^{-1}$nm$^{-1}$]. This value defines the spectrum and radiation rate for a certain spectral band, for instance that of ${\rm N}_2(1{\rm P})$ in Figure 3.6, which includes lines due to a number of vibrational substates. Note that the quantity $A_k$ in (3.1) is in fact the rate integrated across the wavelength range of interest, i.e., $A_k=\int$ $A_k(\lambda)d\lambda$. Photons of all wavelengths enter the detector at rate [s$^{-1}$]

$$\nu_{{\rm det}} = \int \int \Omega {\mathcal F}(\lambda,r)\frac{A}{4\pi r^2}T(\lambda,r) r^2 dr d\lambda$$

$$\* = \int \int \frac{A \Omega {\mathcal F}(\lambda,r)}{4\pi} T(\lambda,r)dr d\lambda,$$

where $T(\lambda,r)$ is the fraction of photons (originating at a given point) which are not scattered or absorbed before reaching the detector (see Section 3.2.2). We divide this incident photon rate by the ``geometric factor'' $A\Omega$ [cm$^2$str] to attain a photometer-independent measure, and by $10^6/4\pi$ for convenience to find once again the surface brightness in Rayleighs,

$$I = \nu_{{\rm det}} \frac{1}{A\Omega}\frac{4\pi}{10^6}$$

$$\* = 10^{-6} \int \int {\mathcal F}(\lambda,r)T(\lambda,r)dr d\lambda.$$ (3.3)

In this form the photon count rate is integrated over all wavelengths and accounts for any transmission losses.

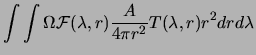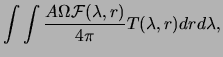Thus the Rayleigh unit provides a measure which is convenient experimentally, via (3.3), and which relates easily via (3.1) to theoretical calculations determining volume emission rates in given molecular bands.

Figure 3.6: Factors affecting the photometric response to the ${\ensuremath{{\rm N}_2(1{\rm P})}}$ and ${\ensuremath{{\rm N}_2(2{\rm P})}}$ optical bands. The band fine structure represents transitions between individual vibrational substates of the electronic states which define the band. The three groups of such spectral peaks discernable in the ${\rm N}_2(1{\rm P})$ spectrum correspond to groups of transitions with the same net change in vibrational excitation number.

We note for reference that to express a surface brightness in W-cm$^{-2}$s$^{-1}$str$^{-1}$, we multiply the value in Rayleighs at wavelength $\lambda$ by $(10^6/2)(\hbar c/\lambda)$, where $\hbar$ and $c$ are the fundamental constants. We thus have,

$$1 {\rm kR} \simeq 22.6 {{\rm pW\hbox{-}cm}^{-2}{\rm s}^{-1}{\rm str}^{-1}} {\rm at } \lambda=700 {\rm nm}$$

$$39.5 {\rm pW\hbox{-}cm}^{-2}{\rm s}^{-1}{\rm str}^{-1} {\rm at } \lambda=400 {\rm nm}$$

Photometric observations are reported as an apparent brightness, without explicit knowledge or consideration of $T(\lambda,r)$. In addition, they typically represent measurements valid over a restricted wavelength range, dependent on the sensor response range. In contrast, theoretical calculations typically report emission intensities integrated over an entire spectral band, based on equation (3.1); for instance, ${\ensuremath {{\rm N}_2(1{\rm P})}}$ spans the wavelength range 575 nm to 2300 nm. An ideal instrument, with spectral resolution, can thus instead provide a more fundamental measure, the spectral surface brightness, given as

$$S(\lambda)= 10^{-6} \int {\mathcal F}(\lambda,r)T(\lambda,r)dr.$$

For instance, the clear night sky background for visible wavelengths is approximately 20 R-nm$^{-1}$ without the moon and 60 R-nm$^{-1}$ with a full moon [Gary Swenson, private communication, 1995]. Note that $I=\int S(\lambda)d\lambda$.

3.3.2 Calibration

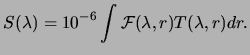
A real photometer responds with a count rate somewhat less than that given by equation (3.3), depending on the quantum efficiency of the detector. The voltage response $V_{\rm obs}$ of a photosensitive device, for instance the anode of a photomultiplier or a pixel of an intensified CCD, is given by

$$V_{\rm obs}= \ensuremath{G_{V_{{\rm H{}}}}}\frac{10^6}{4\pi} A \Omega \int_{\lambda} S(\lambda)f(\lambda)q(\lambda)d\lambda$$ (3.4)

where

$\ensuremath{G_{V_{{\rm H{}}}}}$

is the gain, measured in volts per photoelectron-s$^{-1}$, of the proportional photometer (and amplifier) when operated with a high-voltage of $V_{{\rm H{}}}$,

$A\Omega$

is the geometric factor for the photometer, where $A$ is its aperture and $\Omega$ is the smaller of the solid angles subtended by either the photometer's field-of-view or the extent of the light source,

$S(\lambda)$

is the apparent spectral surface brightness at wavelength $\lambda$, measured in Rayleighs (R) per nm,

$f(\lambda)$

is the fractional transmittance of any optical filters, and

$q(\lambda)$

is the quantum efficiency of the photometer's photocathode.

When making broadband optical measurements of a source whose optical output may vary with wavelength, we cannot unambiguously determine the optical intensity if the instrumental $q(\lambda)$ also varies with wavelength. Thus to express experimental intensities based on (3.4) we assume that

$$S(\lambda)=I \; \delta(\lambda - \lambda _0)$$ (3.5)

where $\delta(\cdot)$ is the Dirac delta function and $\ensuremath{{\lambda_0}}$ is an appropriate wavelength which dominates the integral in (3.4). Observations can then be calibrated and expressed at the chosen wavelength $\ensuremath{{\lambda_0}}$ by

$$\ensuremath{{I_{\ensuremath{{\lambda_0}}} }} = \frac{V_{\rm obs}\ensuremath{G_{V_{{\rm H{(cal)}}}}}[A\Omega]_{\r... ...\rm obs} \: f(\ensuremath{{\lambda_0}})q(\ensuremath{{\lambda_0}})V_{\rm cal} }$$

$$\* = \alpha_{\ensuremath{{\lambda_0}}} V_{\rm obs}\frac{\ensuremath{G_{V_{{\rm H{(cal)}}}}}}{\ensuremath{G_{V_{{\rm H{(obs)}}}}}}$$

$$\* = \alpha_{\ensuremath{{\lambda_0}}} V_{\rm obs}\left(\frac{\ensuremath{V_{{\rm H{(cal)}}}}}{\ensuremath{V_{{\rm H{(obs)}}}}}\right)^\epsilon$$ (3.6)

where we have assumed that $\ensuremath{G_{V_{{\rm H{}}}}}$ is proportional to $(\ensuremath{V_{{\rm H{}}}})^\epsilon$ for some $\epsilon$, as is true for electron multipliers such as photomultipliers or multichannel plates, and we have defined the calibration factor

$$\alpha_{\ensuremath{{\lambda_0}}} \equiv \frac{ [A\Omega]_{\rm ca... ..._{\rm obs} f(\ensuremath{{\lambda_0}})q(\ensuremath{{\lambda_0}})V_{\rm cal} }.$$ (3.7)

Here the value $\ensuremath{{I_{\ensuremath{{\lambda_0}}} }}$ is averaged over the entire field-of-view of the photometer or pixel.

In summary, to calibrate a broadband photometer we must choose an appropriate wavelength $\ensuremath{{\lambda_0}}$ which dominates the integral in (3.4), determine the calibration factor $\alpha_{\ensuremath{{\lambda_0}}}$ for that wavelength, and determine the instrument gain behavior (e.g. the value of $\epsilon$) in order that a variety of gains can be used in observations.

3.3.3 Band brightness at the source

The measure of optical intensity discussed above is used in this work because, although not an accurate count of photon flux, it does not require any assumptions about the optical spectrum under observation. However, as can be seen from Figure 3.6, the expected responses to sprite luminosity in our instrument are dominated by narrow spectral ranges. For blue photometers sensitive to the ${\rm N}_2(2{\rm P})$ band, the dominant wavelength region is near 375 to 400 nm and is determined mostly by the competing factors of the atmospheric transmission and the blue filter response. For red photometers, the PMT (photocathode) response and the longpass red filter select a portion of the ${\rm N}_2(1{\rm P})$ spectrum near 700 nm. The dominance of a narrow spectral region in each photometer justifies the use of equation (3.5) and endows the measure $\ensuremath{{I_{\ensuremath{{\lambda_0}}} }}$ with physical significance. ${I_{\ensuremath{{\lambda_0}}} }$ can be taken to be an approximate measure of the true brightness near the dominant optical wavelength ${\lambda_0}$.

A more direct experimental comparison with the theoretical surface brightness of equation (3.1) can be made if (1) one band strongly dominates the instrument response, (2) its spectrum $A_k(\lambda)$ is known, and (3) the atmospheric transmission $T(\lambda,r)$ is known.

From these assumptions and equations (3.2), (3.4), (3.5), and (3.6), the total source brightness in band $k$ can be inferred from a wideband measurement:

$$I_k = A_k \ensuremath{{I_{\ensuremath{{\lambda_0}}} }}\frac{f(\en... ...math{{\lambda_0}})}{\int A_k(\lambda) T(\lambda,r)f(\lambda)q(\lambda)d\lambda}$$

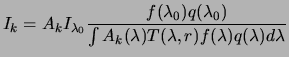In a similar manner, the relative excitation rate of two bands can be assessed through two-color photometry. For instance, the red and blue optical filters shown in Figure 3.6 can be used to assess the average excitation ratio of states ${{\rm C}^3\Pi_{\rm u}}$ and ${{\rm B}^3\Pi_{\rm g}}$ through their emissions in the ${\ensuremath {{\rm N}_2(1{\rm P})}}$ and ${\ensuremath {{\rm N}_2(2{\rm P})}}$ bands.

$$\Bigl\langle\frac{n_{_{\ensuremath{{{\rm C}^3\Pi_{\rm u}}}}}}{n_{_\ensuremath{{{\rm B}^3\Pi_{\rm g}}}}}\Bigr\rangle \equiv \frac{\int A_{_{{\rm N}\!_2\!1\!{\rm P}}} n_{_\ensuremath{{{\rm C... ...int A_{_{{\rm N}\!_2\!2\!{\rm P}}} n_{_\ensuremath{{{\rm B}^3\Pi_{\rm g}}}} dr}$$

$$= \frac{I_{700}}{I_{400}} \; \frac{f(700 {\rm nm})q(700 {\rm nm})}{... ...{{\rm N}\!_2\!1\!{\rm P}}}\!(\lambda) T(\lambda,r)f(\lambda)q(\lambda)d\lambda}$$ (3.8)

where $I_{700}$ and $I_{400}$ are observed surface brightnesses expressed according to equation (3.6) for wavelengths 700 nm and 400 nm.