| 0 | (1.1) | ||
| (1.2) | |||
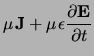 |
(1.3) | ||
| (1.4) |
The subject treated in this dissertation lends itself to analysis
largely by classical electrodynamics. As a result, Maxwell's equations
are fundamental to much of the theoretical discussion. The Système Internationale or ``rationalized MKS'' units are used
throughout. In differential form, Maxwell's noble laws for
electromagnetic fields are:
The force exerted on a non-relativistic charged particle of mass ![]() and
charge
and
charge ![]() due to these fields is given by the Lorentz force equation,
due to these fields is given by the Lorentz force equation,
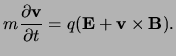 |
(1.5) |
Under conditions of high charged particle density and number, a group
of charged particles takes on the properties of a plasma and may be
described by its collective behavior. By defining a
distribution function
![]() describing the
time-dependent occupation of phase space for each kind of charged
particle, the Boltzmann equation
describing the
time-dependent occupation of phase space for each kind of charged
particle, the Boltzmann equation